CORRECTION DU DM 5 1ère SPE C MATHS 2

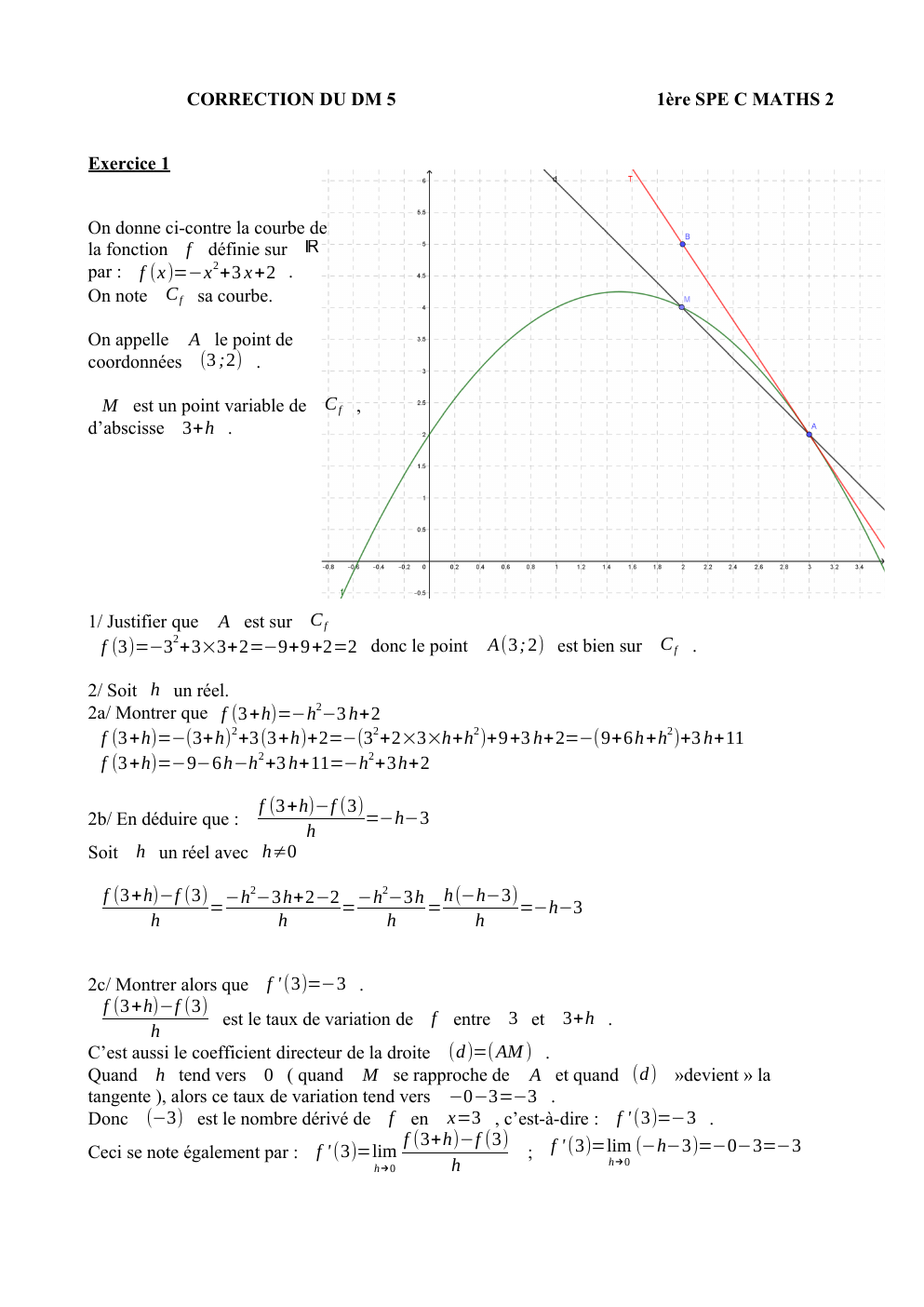
« CORRECTION DU DM 5 1ère SPE C MATHS 2 Exercice 1 On donne ci-contre la courbe de la fonction f définie sur ℝ par : f (x )=−x 2 +3 x +2 . On note C f sa courbe. On appelle A le point de coordonnées (3 ;2) . M est un point variable de C f , d’abscisse 3+h . 1/ Justifier que A est sur C f 2 f (3)=−3 +3×3+2=−9+9 +2=2 donc le point A(3 ; 2) est bien sur C f . 2/ Soit h un réel. 2a/ Montrer que f (3 +h)=−h2−3 h+2 f (3 +h)=−(3+h)2 +3 (3 +h)+2=−(32 +2×3×h+h2 )+9 +3 h+2=−(9+6 h +h2 )+3 h+11 2 2 f (3 +h)=−9−6 h−h +3 h+11=−h +3 h+2 f (3 +h)−f (3) =−h−3 h Soit h un réel avec h≠0 2b/ En déduire que : f (3 +h)−f (3) −h2−3 h+2−2 −h2−3 h h (−h−3) = = = =−h−3 h h h h 2c/ Montrer alors que f ' (3)=−3 . f (3 +h)−f (3) est le taux de variation de f entre 3 et 3+h . h C’est aussi le coefficient directeur de la droite (d )=( AM ) . Quand h tend vers 0 ( quand M se rapproche de A et quand (d ) »devient » la tangente ), alors ce taux de variation tend vers −0−3=−3 . Donc (−3) est le nombre dérivé de f en x=3 , c’est-à-dire : f ' (3)=−3 . f (3+h)−f (3) (−h−3)=−0−3=−3 Ceci se note également par : f ' (3)=lim ; f ' (3)=lim h→0 h h→0 3/ On appelle (T ) la tangente à C f en x=3 . 3a/ Montrer que (T ) a pour équation : y =−3 x+11 . La tangente à C f en x=a a pour équation : y =f '(a)( x−a)+f (a) . Ici, a=3 donc (T ) a pour équation : y =f '(3)( x−3)+f (3) . Or f ' (3)=−3 et f (3)=2 , donc l’équation de (T ) est : y =−3 (x −3)+2=−3 x +9+2=−3 x +11 3b/ Tracer (T ) sur le graphique. x y =−3 x+11 0 1 −3×0+11=11 −3×1+11=8 2 −3×2+11=5 3 −3×3+11=2 4 −3×4+11=−1 (T ) passe par les points de coordonnées : (0 ;11) , (1 ; 8) , (2 ; 5) , (3 ;2) et (4 ;−1) .

On retrouve bien sûr que (T ) passe par le point A=(3 ; 2) . Sur le graphique, on a la place pour placer le point de coordonnées B=(2 ; 5) . (T ) est alors la droite ( AB) . 4a/ Vérifier que pour tout réel x , on a : f (x )−(−3 x +11)=−x 2 +6 x−9 2 2 2 f (x )−(−3 x +11)=−x +3 x +2−(−3 x +11)=−x +3 x +2+3 x−11=−x +6 x−9 4b/ Déterminer le tableau de signes sur ℝ de l’expression (− x2 +6 x−9) . (− x2 +6 x−9) est une expression du 2nd degré.

Δ=62 −4×(−1)×(−9)=36−36=0 . −6 −6 = =3 . Une seule racine : x 0= 2×(−1) −2 −∞ +∞ x 3 Signe de (− x2 +6 x−9) - 0 - 4c/ En déduire que pour tout réel x , on a : f (x )⩽−3 x +11 . Interpréter ce résultat sur le graphique. D’après le tableau de signes, on peut dire que pour tout réel x : (− x2 +6 x−9)⩽0 . Donc, pour tout réel x , on a : f (x )−(−3 x +11)⩽0 , soit f (x )⩽−3 x +11 . Ainsi, C f est toujours située en-dessous de (T ) , éventuellement croise (T ) . Remarque : C f croise (T ) quand f (x )=(−3 x +11) , soit quand f (x )−(−3 x +11)=0 . Ainsi, C f croise (T ) quand (− x2 +6 x−9)=0 , soit quand x=3 . C f ne croise (T ) que quand x=3 , c’est-à-dire au point A . En dehors du point A , C f est toujours située strictement en-dessous de (T ) . Exercice 2 On donne ci-après la courbe d’une fonction g dérivable sur ℝ .

On note C g cette courbe. Les points A=(0 ; 1) , B=(1 ;1,5) et C=(−1 ;−0,5) sont sur C g . On a tracé (T 1) et (T 2) , les tangentes à C g , respectivement aux points A et B . (T 1) a pour équation : y =2 x +1 ; (T 2) passe par le point R(0; 2) . 1a/ Calculer g ' (0) . g ' (0) est le coefficient directeur de la tangente à C g en x=0 , donc au point Cette tangente est la droite (T 1) , d’équation : y =2 x +1 . Par conséquent, le coefficient directeur de (T 1) est 2 . Ainsi : g ' (0)=2 . A . 1b/ Déterminer une équation de (T 1) . La tangente à C g en x=a a pour équation : y =g ' (a)(x −a)+ g (a) . Ici, a=0 et cette tangente s’appelle (T 1) . Donc (T 1) a pour équation : y =g ' (0)( x−0)+ g(0)=g ' (0)×x + g(0) . Or g ' (0)=2 d’après la question précédente. Ensuite, le point A=(0 ; 1) est sur C g , donc g(0)=1 . Ainsi, (T 1) a pour équation : y =2 x +1 . 2/ Quel autre nombre dérivé de g peut-on donner avec les informations de l’énoncé ? (T 2) est la tangente à C g au.... »